martes, 10 de julio de 2012

Un conjunto es una coleccion bien definida de objetos a los cuales tambien llamamos los elementos de un conjunto.
A los conjuntos los identificamos con letras mayusculas y a los elementos con letras minusculas, encerrados en {}.
los conjuntos se pueden describir de 2 formas:
1.- metodo de la lista. consiste en enumerar a todos los elementos que pertenecen a dicho conjunto. ejemplo:

A={1,2,3,4,5,6} B={a,e,i,o,u}
2.- metodo de la regla consiste en definir la caracteriztica comun para ser considerado un elemento. ejemplo.

A= x b= {x|x sea una letra vocal

Definición y notación de un conjunto


A los conjuntos se les representa con letras mayúsculas A, B, C, ... y a los elementos de los conjuntos  se denotan con letra minúsculas a, b, c, ...En base a la cantidad de elementos que tenga un conjunto, estos se pueden clasificar en conjuntos

Ejemplo : Supongamos que Venezuela es un conjunto, los elemento de ella son todos los estados.

finitos e infinitos.En el caso del ejemplo anterior Venezuela es un conjunto finito ya que se pueden contar sus elementos.
Podemos definir de manera intuitiva a un conjunto, como una colección o listado de objetos con
características bien definidas que lo hace pertenecer a un grupo determinado.
Para que exista un conjunto debe basarse en lo siguiente:
  • La colección de elementos debe estar bien definida.
  • Ningún elemento del conjunto se debe contar más de una vez, generalmente, estos elementos deben ser diferentes, si uno de ellos se repite se contará sólo una vez.
  • El orden en que se enumeran los elementos que carecen de importancia.

Operaciones y leyes de conjuntos3.1.2.1 Unión. La unión de los conjuntos A y B, es el conjunto de todos los elementos que pertenecen a A o a B o a ambos. Se denota la unión de A y B por A + B y se llama unión de A y B.
En consecuencia,



x Î ( A + B) Û x Î A Ú x Î B.




Entonces se puede expresar por comprensión este conjunto así:


A + B = {x / x Î A Ú x Î B }


Una interpretación gráfica de la unión de A y B es la siguiente:



En la gráfica la región rayada corresponde a la unión de A y B. Se presentan los conjuntos dentro de un rectángulo que representa el conjunto referencial del cual se seleccionan los conjuntos A y B.
Leyes del Álgebra de Conjuntos.

Si 1 designa al conjunto universal y 0 al conjunto vacío, las siguientes identidades son válidas en el álgebra de conjuntos para conjuntos arbitrarios X, Y, Z.

Leyes conmutativas


XY = YX               X + Y = Y + X.



Leyes asociativas


X(YZ) = (XY)Z               X + (Y + Z) = (X + Y) + Z.



Leyes distributivas


X(Y + Z) = XY + XZ               X + YZ = (X + Y) (X + Z).



Leyes de idempotencia


XX = X               X + X = X.



Leyes de complementación


XX' = 0               X + X' = 1.



Leyes de absorción


X (X + Y) = X               X + XY = X.



Leyes de D'Morgan


( XY)' = (X' + Y')               (X + Y )' = X'Y'.



Leyes con 0 y 1


X 1 = X               X + 0 = X.
X 0 = 0               X + 1 = 1.
0' = 1               1' = 0.



Ley de complemento doble


(X')' = X.


 
Es importante destacar la dualidad dada en estas leyes, es decir, si en cualquiera de las identidades, cada unión se reemplaza por una intersección, cada intersección por una unión, cada 0 por 1 y cada 1 por 0, la expresión resultante es también una identidad.

Diagramas de Venn Euler



Un diagrama de Euler es una manera diagramática de representar a los conjuntos y sus relaciones. Son una representación moderna de los círculos de Euler, los cuales deben su nombre a su creador, Leonhard Euler.
Los diagramas de Euler normalmente consisten de simples curvas cerradas en el plano que son usadas para describir conjuntos. Las relaciones espaciales entre las curvas (superposición, contención o ninguno) corresponden, respectivamente, a relaciones de intersección, subconjunto y disjuntes, de la teoría de conjuntos.
Estos diagramas son una generalización del bien conocido diagrama de Venn, el cual representa todas las posibles intersecciones entre los conjuntos presentes dados.
A la intersección del interior de una colección de curvas con el exterior del resto de curvas se le llama zona. Así, dado un conjunto de curvas, en los diagramas de Venn todas las zonas deben estar presentes, pero no así en un diagrama de Euler, donde algunas zonas podrían no estar.
En el sentido de la lógica, uno puede usar la semántica de un modelo teórico para interpretar los diagramas de Euler dentro de un dominio de discurso. En el ejemplo de la figura, el diagrama de Euler representa que los conjuntos Animal y Mineral son disjuntos, porque las curvas correspondientes son disjuntas, y también que el conjunto Four Legs es un subconjunto del conjunto Animal. El diagrama de Venn que usa las mismas categorías Animal, Mineral y Four Legs no encapsula esta información. Tradicionalmente, este vacío de un conjunto en los diagramas de Venn es descrito por un sombreado o achurado de la región.
Los diagramas de Euler, en cambio, representan vacío ya sea por el sombreado o por la omisión de una de las zonas.
A menudo se impone un conjunto de condiciones bien formadas, que corresponden a restricciones topológicas o geométricas impuestas a la estructura del diagrama. Por ejemplo, se puede forzar la conectitud de las zonas, o prohibir la concurrencia de curvas o puntos múltiples como forma de representar intersecciones tangenciales de curvas. En el diagrama de abajo, se observa la transformación secuencial de pequeños diagramas de Venn en diagramas de Euler; algunos de los diagramas intermedios tienen concurrencia de curvas. Sin embargo, esta secuencia de transformaciones desde un diagrama de Venn con sombreado hasta un diagrama de Euler sin sombreado, no es siempre posible. En efecto, existen ejemplos de diagramas de Euler con 9 conjuntos que no son diagramables usando curvas cerradas simples y sin la creación de zonas no deseadas, puesto que ellos tendrían que tener grafos duales no planares.

Principios aditivo y multiplicativo. Diagrama de árbol


PRINCIPIO MULTIPLICATIVO.

Permutaciones

llamamos permutación de un conjunto a cada una de las posibles ordenaciones de todos los elementos de dicho conjunto.
Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
La definición intuitiva de permutación, como ordenamientos o arreglos de los elementos de un conjunto se formaliza con el uso del lenguaje de funciones matemáticas.



Una permutación de un conjunto X es una función biyectiva de dicho conjunto en sí mismo.


Ejemplo de permutación considerada como función biyectiva.
Para ilustrar la definición, retomemos el ejemplo descrito en la introducción. En el ejemplo, X={1, 2, 3}.
Entonces, cada correspondencia uno a uno entre el conjunto {1, 2, 3} a sí mismo equivale a una forma de ordenar los elementos.
Por ejemplo, la asignación biyectiva dada por
  • 1 → 1
  • 2 → 2
  • 3 → 3
puede hacerse corresponder al ordenamiento "1, 2, 3".
Por otro lado, la asignación biyectiva dada por
  • 1 → 3
  • 2 → 2
  • 3 → 1

puede hacerse corresponder al ordenamiento "3, 2, 1".
En la definición de permutación, no se establece condición alguna sobre X, el cual puede incluso ser infinito. Sin embargo, es común considerar únicamente el caso en que X es un conjunto finito al estudiar permutaciones.


Combinacion
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.

Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de;

N1 x N2 x ……….x Nr maneras o formas
El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.
Ejemplos:
1) Una persona desea construir su casa, para lo cuál considera que puede construir los cimientos de su casa de cualquiera de dos maneras (concreto o block de cemento), mientras que las paredes las puede hacer de adobe, adobón o ladrillo, el techo puede ser de concreto o lámina galvanizada y por último los acabados los puede realizar de una sola manera ¿cuántas maneras tiene esta persona de construir su casa?

PRINCIPIO ADITIVO.
Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ….. y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de,

M + N + ………+ W maneras o formas
Ejemplos:
1) Una persona desea comprar una lavadora de ropa, para lo cuál ha pensado que puede seleccionar de entre las marcas Whirpool, Easy y General Electric, cuando acude a hacer la compra se encuentra que la lavadora de la marca W se presenta en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática o semiautomática, mientras que la lavadora de la marca E, se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser automática o semiautomática y la lavadora de la marca GE, se presenta en solo un tipo de carga, que es de 11 kilogramos, dos colores diferentes y solo hay semiautomática. ¿Cuántas maneras tiene esta persona de comprar una lavadora?

Solución:
M = Número de maneras de seleccionar una lavadora Whirpool
N = Número de maneras de seleccionar una lavadora de la marca Easy
W = Número de maneras de seleccionar una lavadora de la marca General Electric
M = 2 x 4 x 2 = 16 maneras
N = 3 x 2 x 2 = 12 maneras
W = 1 x 2 x 1 = 2 maneras
M + N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora
Publicado por en No hay comentarios:

http://www.youtube.com/watch?v=C5nZ3XIfQ88&NR=1&feature=endscreen

**ESPACIO MUESTRAL**

En la teoría de probabilidades, el espacio muestral o espacio de muestreo (denotado E, S, Ω o U) consiste en el conjunto de todos los posibles resultados individuales de un experimento aleatorio.
Por ejemplo, si el experimento consiste en lanzar dos monedas, el espacio de muestreo es el conjunto {(cara, cara), (cara, cruz), (cruz, cara) y (cruz, cruz)}. Un evento o suceso es cualquier subconjunto del espacio muestral, llamándose a los sucesos que contengan un único elemento sucesos elementales. En el ejemplo, el suceso "sacar cara en el primer lanzamiento", o {(cara, cara), (cara, cruz)}, estaría formado por los sucesos elementales {(cara, cara)} y {(cara, cruz)}.
Para algunos tipos de experimento puede haber dos o más espacios de muestreo posibles. Por ejemplo, cuando se toma una carta de un mazo normal de 52 cartas, una posibilidad del espacio de muestreo podría ser el número (del as al rey), mientras que otra posibilidad sería el palo (diamantes, tréboles, corazones y picas). Una descripción completa de los resultados, sin embargo, especificaría ambos valores, número y palo, y se podría construir un espacio de muestreo que describiese cada carta individual como el producto cartesiano de los dos espacios de muestreo descritos.
Los espacios de muestreo aparecen de forma natural en una aproximación elemental a la probabilidad, pero son también importantes en espacios de probabilidad. Un espacio de probabilidad (Ω, F, P) incorpora un espacio de muestreo de resultados, Ω, pero define un conjunto de sucesos de interés, la σ-álgebra F, por la cuál se define la medida de probabilidad.

**EVENTOS**

un evento o suceso es un subconjunto de un espacio muestral, es decir, un conjunto de posibles resultados que se pueden dar en un experimento aleatorio.
Formalmente, sea Ω un espacio muestral, entonces un evento es un subconjunto A:=\{w_1,w_2,...\}\subseteq\Omega, donde (w_1, w_2, ...) son una serie de posibles resultados.
Se dice que un evento A ocurre, si el resultado del experimento aleatorio es un elemento de A.

TIPOS DE EVENTOS
Evento simple o suceso elemental
Un suceso o evento simple es un subconjunto del espacio muestral que contiene un único elemento.
Ejemplos de espacios muestrales y sucesos elementales:
  • Si se trata de contar objetos y el espacio muestral S = {0, 1, 2, 3, ...} (los números naturales), entonces los sucesos elementales son cada uno de los conjuntos {k}, donde k ∈ N.
  • Si se lanza una moneda dos veces, S = {cc, cs, sc, ss}, donde (c representa "sale cara" y s, "sale cruz"), los sucesos elementales son {cc}, {cs}, {sc} y {ss}.
  • Si X es una variable aleatoria normalmente distribuida, S = (-∞, +∞), los números reales, los sucesos elementales son todos los conjuntos {x}, donde x ∈ \mathbb R.
Los sucesos elementales pueden tener probabilidades que son estrictamente mayores que cero, cero, no definidas o cualquier combinación de estas. Por ejemplo, la probabilidad de cualquier variable aleatoria discreta está determinada por las probabilidades asignadas a los sucesos elementales del experimento que determina la variable. Por otra parte, cualquier suceso elemental tiene probabilidad cero en cualquier variable aleatoria continua. Existen distribuciones mixtas que no son completamente continuas, ni completamente discretas, entre las que pueden darse ambas situaciones.

Otros sucesos

  • Un evento compuesto es un subconjunto \{w_1,...,w_n\}\subseteq\Omega.
  • Los eventos triviales son el conjunto universal Ω y el conjunto vacío. Al primero se le llama también evento seguro, y al segundo, evento imposible.
  • Sean dos eventos A y B, si ambos son conjuntos disjuntos, entonces ellos son eventos excluyentes.
  • Un evento con elementos infinitos pero numerables se llama σ-álgebra (sigma-álgebra), y un evento con elementos finitos se llama álgebra de sucesos de Boole.

**AXIOMAS Y TEOREMAS DE LA PROBABILIDAD**

Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función definida sobre un conjunto de sucesos determine consistentemente sus probabilidades. Fueron formulados por Kolmogórov en 1933.

Axiomas de Kolmogórov:

Primer axioma:

La probabilidad de que ocurra un evento A cualquiera se encuentra entre cero y uno.

0 £ p(A) ³ 1

Ejemplo: La probabilidad de sacar par en un dado equilibrado es 0,5. P(A)=0,5

Segundo Axioma:

La probabilidad de que ocurra el espacio muestral d debe de ser 1.

                                                           p(d) = 1

Ejemplo: La probabilidad de sacar un número del 1 al 6 en un dado equilibrado es "1".

Tercer Axioma: 

Si A y B son eventos mutuamente excluyentes, entonces la,

p(AÈB) = p(A) + p(B)

Ejemplo: La probabilidad de sacar en un dado "as" o sacar "número par" es la suma de las probabilidades individuales de dichos sucesos.

Según este axioma se puede calcular la probabilidad de un suceso compuesto de varias alternativas mutuamente excluyentes sumando las probabilidades de sus componentes.

Generalizando:

Si se tienen n eventos mutuamente excluyentes o exclusivos A1, A2, A3,.....An, entonces;

                               p(A1ÈA2È.........ÈAn) = p(A1) + p(A2) + .......+ p(An)


Ejemplo:

Para el experimento aleatorio de tirar un dado, el espacio muestral es W = {1, 2, 3, 4, 5, 6}. En este espacio el conjunto de sucesos es P(W) = {Æ, {1}, {2}, ...{1,2}, {1,3}, ...{1,2,3,4,5,6}}. Para establecer una probabilidad hay que asignar un número a todos esos sucesos.
Sin embargo si se ha asignado a los sucesos elementales p({1})= p({2})= ...= p({6})= 1/6, por la propiedad ii), p.e. la probabilidad del suceso {1, 3} es p({1,3})= p({1})+ p({3})=2/6.

Nota: El suceso {1} es: "el resultado de tirar el dado es la cara 1", el suceso {1, 3} es: "el resultado de tirar el dado es la cara 1, o la 3", el suceso {1, 3, 5} es: "el resultado de tirar el dado es una cara impar".


TEOREMAS

TEOREMA 1. Si f es un evento nulo o vacío, entonces la probabilidad de que ocurra f debe ser cero.

p(f)=0
 
  
Ejemplo : La probabilidad de que un estudiante sea mujer es "1 menos la probabilidad de que no sea varón". 

DEMOSTRACIÓN:
Si sumamos a fun evento A cualquiera, como f y A son dos eventos mutuamente excluyentes, entonces p(AfÈ)=p(A) +p(f)=p(A). LQQD

TEOREMA 2. La probabilidad del complemento de A, Ac debe ser,

p(Ac)= 1 – p(A).

DEMOSTRACIÓN:
Si el espacio muestral d, se divide en dos eventos mutuamente exclusivos, A y Ac luego d=AÈAc, por tanto p(d)=p(A) + p(Ac) y como en el axioma dos se afirma que p(d)=1, por tanto, p(Ac)= 1 - p(A) .LQQD

TEOREMA 3. Si un evento A Ì B, entonces la p(A) £ p(B).

DEMOSTRACIÓN:
Si separamos el evento B en dos eventos mutuamente excluyentes, A y B \ A (B menos A), por tanto, B=AÈ(B \ A) y p(B)=p(A) +p(B \ A), luego entonces si p(B \ A)³0 entonces se cumple que p(A)£p(B). LQQD

TEOREMA 4. La p( A \ B )= p(A) – p(AÇB)

DEMOSTRACIÓN: Si A y B son  dos eventos cualquiera, entonces el evento A se puede separar en dos eventos mutuamente excluyentes, (A \ B) y AÇB, por tanto, A=(A \ B)È(AÇB), luego p(A)=p(A \ B) + p(AÇB), entonces, p(A \ B) = p(A) – p(AÇB).  LQQD

TEOREMA 5. Para dos eventos A y B, p(AÈB)=p(A) + p(B) – p(AÇB).

DEMOSTRACIÓN:
Si AÈB = (A \ B) È B, donde (A \ B) y B son eventos mutuamente excluyentes, por lo que p(A È B) = p(A \ B) + p(B) y del teorema anterior tomamos que p(A \ B) = p(A) – p(AÇB), por tanto, p(AÈB) = p(A) + p(B) – p(AÇB).  LQQD.

**ESPACIOS FINITOS Y EQUIPARABLES** 

Sea d un espacio muestral que contiene n elementos, d = {a1, a2, a3,....,an}, si a cada uno de los elementos de d le asignamos una probabilidad igual de ocurrencia, pi = 1/n por tener n elementos d, entonces estamos transformando este espacio muestral en un espacio finito equiprobable, el que debe cumplir con las siguientes condiciones:

  1. Las probabilidades asociadas a cada uno de los elementos del espacio muestral deben ser mayores o iguales a cero, pi ³ 0.

  1. La sumatoria de las probabilidades asociadas a cada elemento del espacio muestral debe de ser igual a 1.

Spi = 1

En caso de que no se cumpla con las condiciones anteriores, entonces no se trata de un espacio finito equiprobable.
Solo en el caso de espacios finitos equiprobables, si deseamos determinar la probabilidad de que ocurra un evento A cualquiera, entonces;

            p(A) = r*1/n = r/n

p(A) = maneras de ocurrir el evento A/ Número de elementos del espacio muestral

r = maneras de que ocurra el evento A
1/n = probabilidad asociada a cada uno de los elementos del espacio muestral
n = número de elementos del espacio muestral

**PROBABILIDAD CONDICIONAL**

Es la probabilidad de que ocurra un evento A, sabiendo que también sucede otro evento B. La probabilidad condicional se escribe P(A|B), y se lee «la probabilidad de A dado B».

Interpretación
P(A \mid B) se puede interpretar como, tomando los mundos en los que B se cumple, la fracción en los que también se cumple A. Si el evento B es, por ejemplo, tener la gripe, y el evento A es tener dolor de cabeza, P(A \mid B) sería la probabilidad de tener dolor de cabeza cuando se está enfermo de gripe.
Gráficamente, si se interpreta el espacio de la ilustración como el espacio de todos los mundos posibles, A serían los mundos en los que se tiene dolor de cabeza y B el espacio en el que se tiene gripe. La zona verde de la intersección representaría los mundos en los que se tiene gripe y dolor de cabeza P(A \cap B). En este caso P(A \mid B), es decir, la probabilidad de que alguien tenga dolor de cabeza sabiendo que tiene gripe, sería la proporción de mundos con gripe y dolor de cabeza (color verde) de todos los mundos con gripe: El área verde dividida por el área de B. Como el área verde representa P(A \cap B) y el área de B representa a P(B), formalmente se tiene que:
P(A \mid B) = \frac{P(A \cap B)}{P(B)}.

**PROBABILIDAD TOTAL Y TEOREMA DE BAYES**
 

Probabilidad condicionada. Teorema de Bayes.


Diagrama en árbol, probabilidad condicionada.

**INDEPENDENCIA**

En teoría de probabilidades, se dice que dos sucesos aleatorios son independientes entre sí cuando la probabilidad de cada uno de ellos no está influida por que el otro suceso ocurra o no, es decir, cuando ambos sucesos no están correlacionados.

 Definición formal

Dos sucesos son independientes si la probabilidad de que ocurran ambos simultáneamente es igual al producto de las probabilidades de que ocurra cada uno de ellos, es decir, si P(A \cap B)=P(A)P(B)

 Motivación de la definición

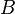Sean A y B dos sucesos tales que P(B)>0, intuitivamente A es independiente de B si la probabilidad de A condicionada por B es igual a la probabilidad de A. Es decir si:
P(A|B) \ = \ P(A)
De la propia definición de probabilidad condicionada:
P(A \mid B) = \frac{P(A \cap B)}{P(B)}.
se deduce que P(A \cap B) \ = \ P(A \mid B) P(B), y dado que P(A|B) \ = \ P(A) deducimos trivialmente que P(A \cap B) \ = \ P(A) P(B).
Si el suceso A es independiente del suceso B, automáticamente el suceso B es independiente de A.

No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder en el tiempo a B, sucederlo o pueden ocurrir simultáneamente. A puede causar B, viceversa o pueden no tener relación causal. Las relaciones causales o temporales son nociones que no pertenecen al ámbito de la probabilidad. Pueden desempeñar un papel o no dependiendo de la interpretación que se le dé a los eventos.

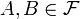Dado un espacio de probabilidad (\Omega, \mathcal F, \mathbb P) y dos eventos (o sucesos) A, B\in \mathcal F con P(B)>0, la probabilidad condicional de A dado B está definida como:

P(A \mid B) = \frac{P(A \cap B)}{P(B)}.

Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)